Liber Primus Cryptanalysis Briefing
Intro
Audience: Experienced Cryptographers seeking a no-fluff primer on LP.
Goal: Rapid familiarization with the structure and framework of LP, as well as current challenges, hypotheses, and methods of attack.
Background: LP is broadly considered the most difficult puzzle of the digital age, and has gone unsolved for over a decade. There are cryptographically sound indications that it is solvable.
Core Facts
Total Pages:
Set 1 (sometimes called LP1): 17 – All solved
Set 2 (sometimes called LP2): 58 – 2 Solved, leaving 56 unsolved
Language:
Runeglish (Rune-English derived from the Gematria Primus)
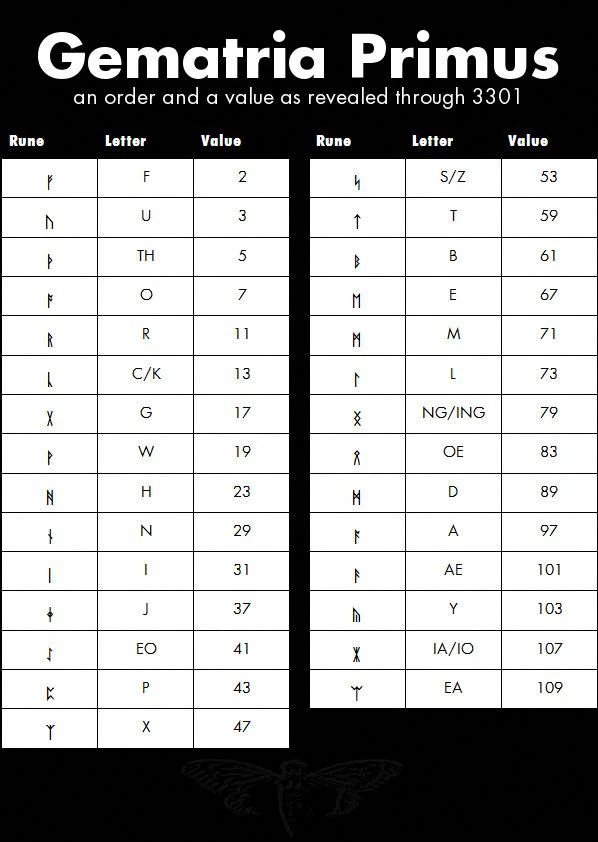
Gematria Primus
Structural Overview
Pagination
LP2’s 58 pages all have numerical names, as defined by 3301 in their May 2014 file dump. The names of the pages are consecutive numerals indexed by 0. i.e. ‘0.jpg,1.jpg,2.jpg…57.jpg’. This is a departure from the nomenclature of LP1.
Segmentation
LP2 consists of multiple ‘sections’, easily recognized by marginalia and rubricated incipits. Stylistically reminiscent of illuminated manuscripts.
Delimiters
1:1 delimiter congruency is assumed to be maintained, as it is in LP1 and the two solved pages of LP2. Liber Primus has unique delimiters used for spaces, line breaks, paragraph, section end, etc. The dot delimiters also correspond to the ASCII control characters LF (Line Feed), CR (Carriage Return), and ETB (End of Transmission Block)
GP Values
GP letter values can be used to construct prime words, phrases, and sentences/lines. Prime/emirp GP sums serve an important role as exemplified by 57.jpg
Artwork
LP contains various forms of both original and existing artwork. 1033.jpg, sometimes called the ‘cover‘ of LP, is a collage of four William Blake pieces: Newton, The Ancient of Days, and two versions of Nebuchadnezzar. Within LP2, ‘sections’ are ostensibly indicated by original marginalia. Specific pages also contain separate, page-relevant original artwork — such as cuneiform numerals or mobius strips. Additionally, several instances of edited artwork from known sources exist — such as the mayfly and oak tree.
Structural Analysis
n-grams
———————————————
LP text:
Counted unique bigrams: 840
Number of repeated bigrams: 837
Total number of repeated bigrams: 12952
Random text:
Mean counted unique bigrams: 840.9997
Std counted unqiue bigrams: 0.01731790980459247
Mean number of repeated bigrams: 840.9963
Std number of repeated bigrams: 0.060714989911882546
Mean total number of repeated bigrams: 12954.9966
Std total number of repeated bigrams: 0.0582103083654433
———————————————
LP text:
Counted unique trigrams: 9945
Number of repeated trigrams: 2508
Total number of repeated trigrams: 5517.0
Random text:
Mean counted unique trigrams: 10050.1294
Std counted unqiue trigrams: 38.91237406841171
Mean number of repeated trigrams: 2433.5345
Std number of repeated trigrams: 31.238108293397026
Mean total number of repeated trigrams: 5337.4051
Std total number of repeated trigrams: 67.1163422274337 (edited)
———————————————
LP text:
Counted unique quadgrams: 12825
Number of repeated quadgrams: 127
Total number of repeated quadgrams: 255
Random text:
Mean counted unique quadgrams: 12835.0622
Std counted unqiue quadgrams: 11.02112204632541
Mean number of repeated quadgrams: 117.2225
Std number of repeated quadgrams: 10.925364696430046
Mean total number of repeated quadgrams: 235.1603
Std total number of repeated quadgrams: 21.93048116002018
———————————————
Bigrams
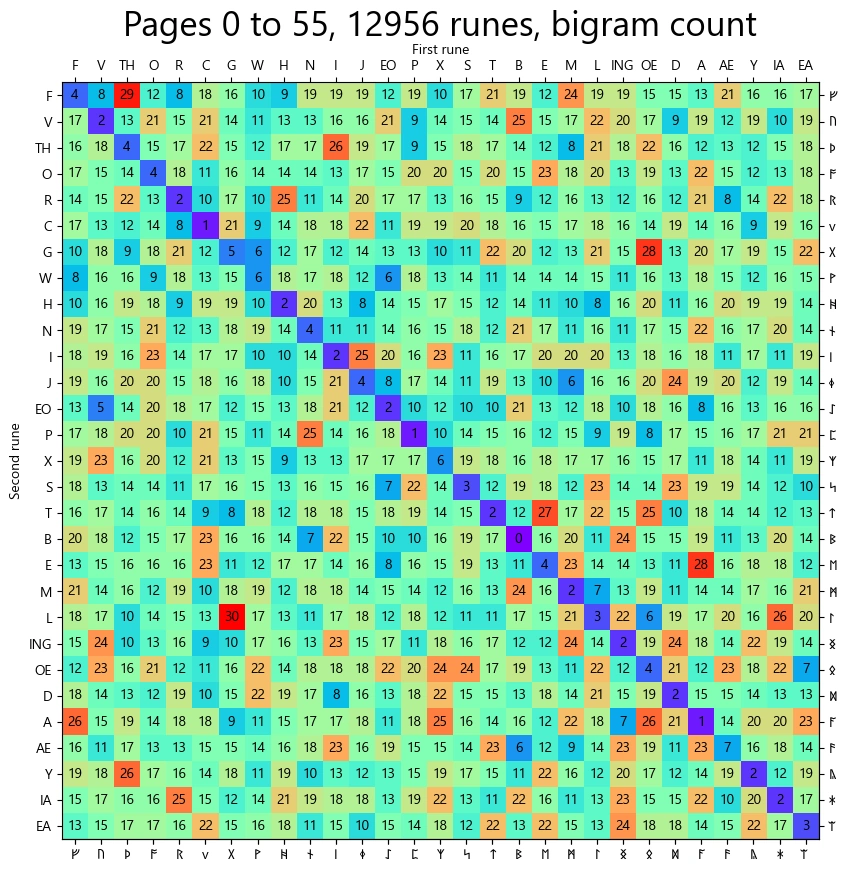
…
Single-rune words
In both sections of the liber primus we see single rune words. From a surface value it seems that these can only be “A”, “I” or possibly “O” based on the William Blake references that we have seen throughout the puzzles. When applying the Gematria Primus, it becomes apparent that single runes can be translated into two or three letter Latin characters such as “TH”, “EO”, “NG/ING”, “OE”, “AE”, “IA/IO”, and “EA”. These additional characters make cribbing much more difficult due to the increase in possibilities that we have to work through.
Dis Legomenon
The 6-gram DJUBEI occurs twice in the corpus of unsolved LP pages, marking the longest such repetition and a possible point of attack.
Character Interchangeability
There is strong evidence to support the encryption was performed on the runes instead of the latin characters. This is due to not being able to go back and forth between runes and latin characters.
An example would be: ᛏᚻᚫᛡ -> THAEIO -> ᚦᚫᛡ
There is more information here.
Progress
15.jpg
15.jpg

The number square on 15.jpg has been mathematically reconstructed. The square is interpretable as the value array for a prime-index recurrence relation of pseudo-fibonacci form. It is also reconstructable via zeckendorf’s theorem.
Analysis of Recent Communications
28th July 2015: Planned Parenthood message. The GP sum of the entire message is 11,570 = 2 × 5 × 13 × 89, four of the first five Fib primes. Also there is the 5-3-2-5-7 spacing or some-such. Possibly the Fib and Prime sequences slightly overlaid, and going in opposite directions? Or two Prime sequences?
6th Jan 2016: LP Is The Way message where the Fibonacci sequence was subtracted cumulatively from 464 (3301’s prime index) and the resultant number was used as a prime index to convert it into a prime (Emphasis on the sequence.) There are other ways to interpret the precise algorithm at use here, frustratingly. On the flip side, there are some interpretations that are very similar to the one used in 15.jpg.
29th April 2017: Beware False Paths message — the GP sum of this message is the next term the algorithm found in the 2016 message, IMO confirming that what was found in the 2016 message is not a coincidence.
To summarise: 3301 like meshing the Prime and Fibonacci sequences together in various ways, so I think it’s definitely worth exploring the Prime-Fibonacci space.
Solved Pages
Along with the 17 solved pages from LP1, the ‘last’ two pages of LP2 have been solved — 56.jpg and 57.jpg
56.jpg

56.jpg was ‘solved’ days-weeks after its release via the following method:
Subtract prime numbers - 1 in order:
decimal[i] = (decimal[i] - (primes[i] - 1)) % 29
i.e.
decimal[0] = (decimal[0] - (2 - 1)) % 29
decimal[1] = (decimal[1] - (3 - 1)) % 29
decimal[2] = (decimal[2] - (5 - 1)) % 29
decimal[3] = (decimal[3] - (7 - 1)) % 29
decimal[4] = (decimal[4] - (11 - 1)) % 29
Note that φ(p) = p - 1, where p is prime and φ is Euler's totient function
Here is the deciphered text:
WITHIN THE DEEP WEB, THERE EXISTS A PAGE THAT HASHES TO
36367763ab73783c7af284446c
59466b4cd653239a311cb7116
d4618dee09a8425893dc7500b
464fdaf1672d7bef5e891c6e227
4568926a49fb4f45132c2a8b4
IT IS THE DUTY OF EVERY PILGRIM TO SEEK OUT THIS PAGE
Note: The referenced hash has never been found.
More information about the deep web hash can be found here.
57.jpg

The text of this page can be directly orthographically transliterated from the Gematria Primus, and as such it was ‘solved’ nearly immediately after its release.
Parable:
Like the instar tunneling to the surface.
We must shed our own circumferences.
Find the divinity within and emerge.
